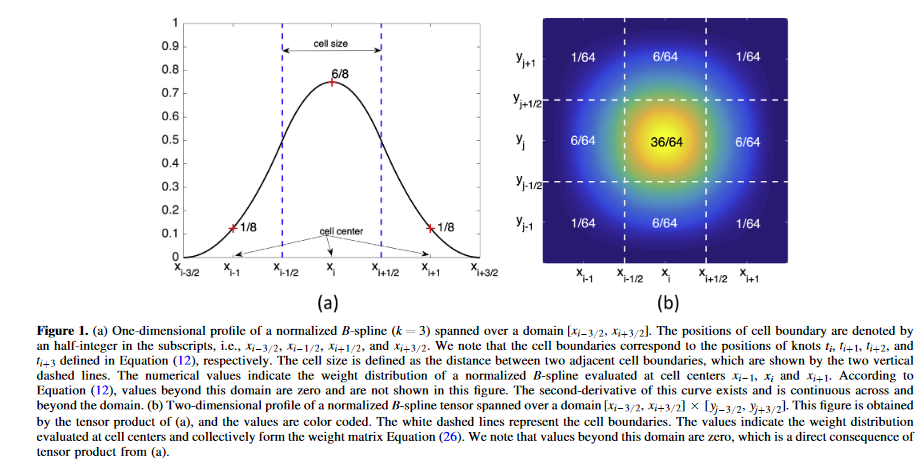
Self-gravitational force calculation for infinitesimally thin disks is important for studies on the evolution of galactic and protoplanetary disks. Although high-order methods have been developed for hydrodynamic and magnetohydrodynamic equations, high-order improvement is desirable for solving self-gravitational forces for thin disks. In this work, we present a new numerical algorithm that is of linear complexity and of high-order accuracy. This approach is fast since the force calculation is associated with a convolution form, and the fast calculation can be achieved using Fast Fourier Transform. The nice properties, such as the finite supports and smoothness, of basis spline functions are exploited to stably interpolate a surface density and to achieve a high-order accuracy in forces. Moreover, if the mass distribution of interest is exclusively confined within a calculation domain, the method does not require artificial boundary values to be specified before the force calculation. To validate the proposed algorithm, a series of numerical tests, ranging from first- to thirdorder implementations, are performed, and the results are compared with analytic expressions derived for thirdand fourth-order generalized Maclaurin disks. We conclude that the improvement on the numerical accuracy is significant with the order of the method, with only little increase of the complexity of the method. [Full article]

 Key words: gravitation – methods: numerica